1D. Complexe getallen
Het complexe vlak
Er bestaan verschillende soorten getallen: gehele getallen, negatieve getallen, breuken en getallen als $\sqrt 2$ en $\pi$. Al deze getallen samen noemen we de reële getallen $\ \large{\mathbb{R}}$. Ze vormen de reële getallenlijn:
Van elk getal $x$ in $\mathbb{R}$ is het kwadraat $x^2$ een positief getal of nul. De vergelijking
$$
x^2=-1
$$
heeft dus geen oplossingen. We maken nu een denkbeeldig (imaginair) getal $i$ waarvoor we afspreken:
$$
i^2=-1.
$$
Helaas, voor $i$ is er geen plaats op de getallenlijn over. In een tweedimensionaal vlak is er echter genoeg ruimte.
We plaatsen het, zoals je hieronder kunt zien, op de positie met coördinaten $(0,1)$.
Op de andere plaatsen komen getallen zoals: $\ -2+3i\ $, $\ -2i\ $ en $\ 1+\sqrt3i$:
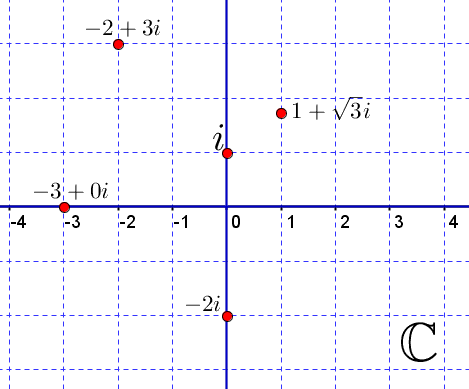
Bij de positie met de coördinaten $(a,b)$ in het bovenstaande vlak hoort dus het getal $a+bi$ waarbij $a$ en $b$ reële getallen zijn.
Al deze getallen samen noemen we de complexe getallen $\ {\mathbb{C}}$.
Complex in de zin van samengesteld; elk complexe getal is immers samengesteld uit twee reële getallen.
De reële getallen zijn zelf ook (een deel van de) complexe getallen; zo kun je het getal $-3$ schrijven als $-3+0i$.
Rekenregels
Twee complexe getallen $a+bi$ en $c+di$ kunnen we optellen met de gewone rekenregels: $$ (a + bi) + (c + di) = a + bi + c + di = (a+c) + (b + d)i, $$ en ook vermenigvuldigen, waarbij we vereenvoudigen door toepassen van $i^2=-1$: $$ (a + bi)\cdot(c + di) = ac + bci + adi + bdi^2 = (ac - bd) + (bc + ad) i. $$ Voor een kwadraat geldt dus: $$ (a+bi)^2=(a+bi)(a+bi)=(a^2-b^2)+2abi. $$ Misschien komen deze regels een beetje uit de lucht vallen maar we zullen ze stuk voor stuk nader toelichten. Om te beginnen met het kwadraat van een complex getal omdat onze hoofdbezigheid tijdens deze webklas het itereren van complexe kwadratische functies is.
Complexe getallen kwadrateren
We kijken hier naar de beweging in het complexe vlak bij het kwadrateren van een complex getal. Eerst een voorbeeld:
Van het getal $z$ hieronder kennnen we de poolcoördinaten, namelijk: $|z|=2$ en $\text{Hoek}(z)=60^{\circ}$.
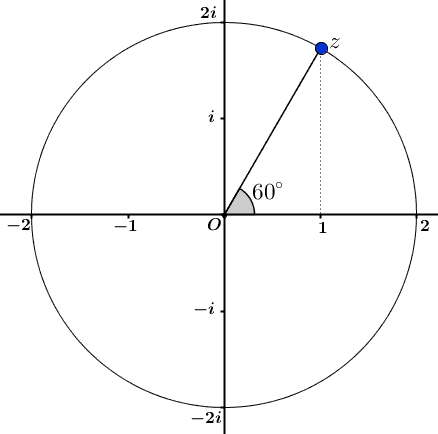
Hoe schrijf je $z$ in de vorm $a+bi$?
Met behulp van goniometrische verhoudingen vinden we:
$$
z=2 \cos(60^{\circ})+2\sin(60^{\circ})i=1+\sqrt3i.
$$
Het kwadraat van $z$ is dan:
$$
z^2=(1+\sqrt3i)\cdot (1+\sqrt3i)=1+3\cdot-1+2\sqrt3i=-2+2\sqrt3i.
$$
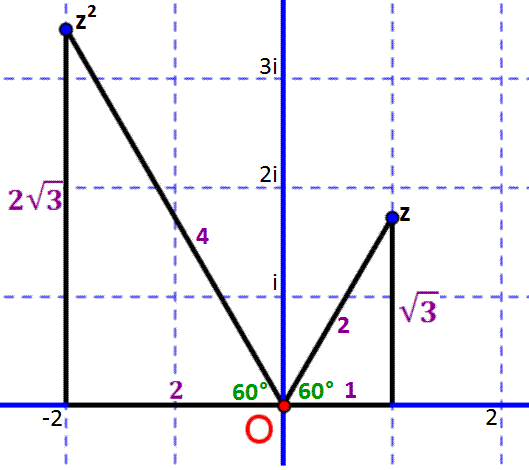
In de afbeelding hierboven staan afstanden in het paars. Bij de overgang van $z$ naar $z^2$ verdubbelt blijkbaar de hoek en wordt de absolute waarde gekwadrateerd. Net als de beweging van de satellieten van Origo! Dat dit voor elk complex getal $z$ geldt bewijzen we hieronder:
Stelling van het kwadrateren in $\mathbb C$
Voor elk complex getal $z$ geldt dat $z^2$, geschreven in poolcoördinaten gelijk is aan: $$ z^2=(|z|^2;\; 2\cdot\text{Hoek}(z)) $$
Bewijs
Zie de figuur hieronder.
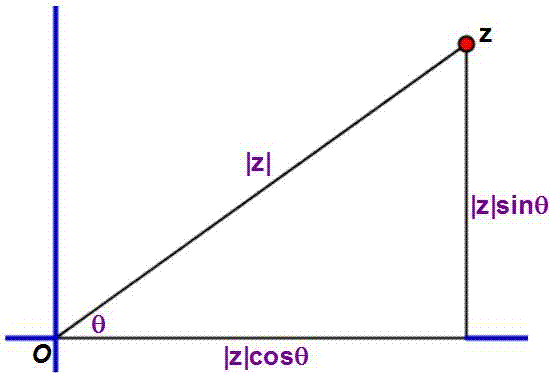
Als Hoek($z$) = $\theta$ dan kunnnen we $z$ schrijven als
$$
|z|\cos\theta+i|z|\sin\theta=|z|(\cos\theta+i\sin\theta),
$$
en dus
$$
z^2=|z|^2(\cos\theta+i\sin\theta)(\cos\theta+i\sin\theta)=|z|^2((\cos^2\theta-\sin^2\theta)+i(2\sin\theta\cos\theta)).
$$
Vanwege de verdubbelingsformules is het laatste gelijk aan:
$$
|z|^2(\cos(2\theta)+i\sin(2\theta))
$$
Hiermee is de stelling bewezen.
Samenvatting en vooruitblik
Uit het bovenstaande volgt dat een iteratiestap van $f(z)=z^2$ net als de beweging van de satellieten van Origo bestaat uit hoekverdubbeling en straal kwadrateren. Voor startwaarden $z_0$ buiten de eenheidscirkel ontsnapt de baan naar het oneindige.
Hieronder hebben we deze startwaarden blauw getekend.

In het rood zie je de startwaarden die een begrensde baan hebben.
Dit rode gebied noemen we de gevulde Juliaverzameling van $f(z)=z^2$.
Het verrassende (en mooie!) is dat je voor andere complexe functies hele grillige plaatjes krijgt, zoals bijvoorbeeld in het plaatje hieronder:

Het gaat hier om de functie $f(z)=z^2-0,6+1,2i$ waarbij je in het rood weer de startwaarden ziet met een begrensde baan. Volgende week veel meer hierover!
Geen parabool
Verwar de complexe functie $f(z)=z^2$ niet met de reële functie $f(x)=x^2$. Van deze laatste kun je een grafiek tekenen, een dalparabool.
Maar voor $f(z)=z^2$ heb je hiervoor 4 dimensies nodig. Als je toch een voorstelling bij deze functie wil maken zou je kunnen proberen
om het volgende plaatje te begrijpen:
Waarom complexe getallen?
Complexe getallen worden vanaf de 17 eeuw gebruikt om makkelijker te kunnen werken met vergelijkingen zoals
\[
x^4 + 2x^3 - 3x + 17 = 0.
\]
De oplossingen van zo'n vierde graads vergelijking kun je vinden met behulp van wortels, maar daarbij is het ontzettend handig als je kunt werken met wortels van negatieve getallen. De 17e eeuwse wiskundigen beschouwden complexe getallen als ontzettend moeilijk en niet bestaand, Descartes noemde ze daarom imaginaire getallen. Pas later is de notatie $a + bi$ in gebruik geraakt en veranderde de naamgeving, $b$ werd het imaginaire deel en $a$ het reële deel. Omdat een complex getal bestaat uit twee delen werden ze niet meer imaginaire getallen maar complexe getallen genoemd. Het woord complex staat dus niet voor ingewikkeld, maar voor bestaand uit meerdere delen.
Tegenwoordig zijn complexe getallen gemeengoed geworden in de wiskunde en worden ze ook in bijvoorbeeld de natuurkunde ontzettend veel gebruikt. Vaak is het eenvoudiger om vergelijkingen eerst te beschouwen over de complexe getallen, zelfs als je alleen geinteresseerd bent in de reële oplossingen. Hoewel het aantal toepassingen enorm is toegenomen is de reden om met complexe getallen te werken nog niet zo anders dan vierhonderd jaar geleden.