1C. De satellieten van de planeet Origo
Om het kwadrateren van complexe getallen te verduidelijken reizen we eerst naar de planeet Origo. We zien hieronder de planeet aangegeven met de letter $O$.
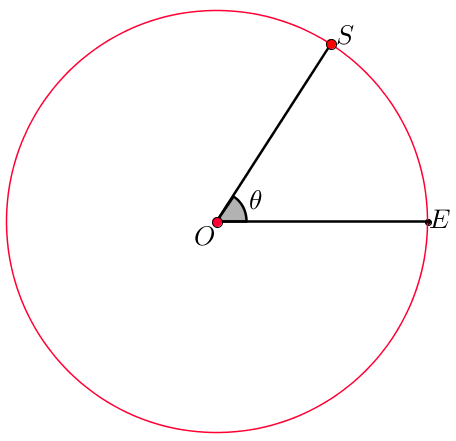
Om deze planeet beweegt de satelliet $S$ zodanig dat de hoek $\theta =\angle SOE $ elke dag verdubbelt. Anders gezegd: de baan van $S$ krijgen we door
te itereren met de functie:
$$
f(\theta)=2\theta
$$
waarbij we de griekse letter $\theta$ uitspreken als "theta".
Welke baan dit oplevert bij een starthoek van $40^{\circ}$ bekijken we hieronder.
Een periodieke baan
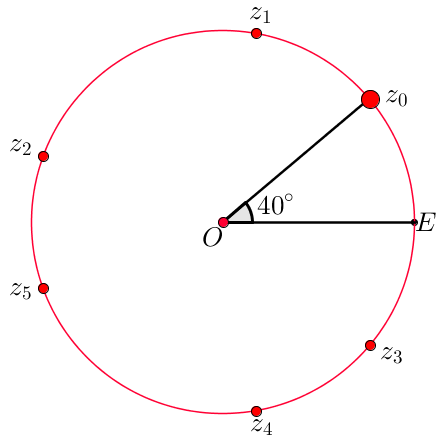
Hieronder zie je de baan bij een starthoek van $40^{\circ}$:
Eerst iets over de notatie. Tot nu toe gaven we banen aan met:
$$
x_0, x_1, x_2, x_3, x_4,\ldots
$$
Het ging hier om een beweging op de (reële ) getallenlijn. Nu bewegen we echter in een tweedimensionaal vlak. In dit geval zullen we de baan aangeven met:
$$
z_0, z_1, z_2, z_3, z_4,\ldots
$$
Nu terug naar de baan bij een starthoek van $40^{\circ}$. Het begin is makkelijk, steeds de hoek verdubbelen:
$$
40^{\circ}, 80^{\circ},160^{\circ},320^{\circ}
$$
Als we nu weer verdubbelen passeren we het punt $E$ en krijgen we
$$
z_4=2\cdot320^{\circ}=640^{\circ}\equiv 640^{\circ}-360^{\circ}=280^{\circ}
$$
Met het symbool "$\equiv$" wordt hier "komt overeen met" bedoeld. Net iets gemakkelijker gaat het zo:
$$
z_4=2\cdot320^{\circ}=2\cdot(360^{\circ}-40^{\circ})\equiv -80^{\circ}
$$
Met een negatieve hoek bedoelen we hier het draaien met de klok mee vanaf $OE$.
De baan wordt dus:
$$
40^{\circ}, 80^{\circ},160^{\circ},-40^{\circ},-80^{\circ},-160^{\circ},-320^{\circ}
$$
Ho, stop! Er geldt:
$$
-320^{\circ}\equiv 40^{\circ}
$$
De starthoek is ook $40^{\circ}$ dus vanaf hier begint alles van voor af aan. De baan van $40^{\circ}$ is dus de eindeloze herhaling van de cyclus:
$$
40^{\circ}, 80^{\circ},160^{\circ},320^{\circ},280^{\circ},200^{\circ}
$$
De baan is periodiek met periode 6. We zeggen dat de positie van $40^{\circ}$ een periodiek punt is met periode 6. Net zo zijn $80^{\circ},160^{\circ},200^{\circ},280^{\circ}$ en $320^{\circ}
$ periodiek met periode 6.
Om over na te denken
Er zijn in totaal 54 periodieke punten met periode 6. Hoe vind je deze?
Satelliet uit koers
Hoe beweegt een satelliet waarvan de afstand tot $O$ ongelijk is aan $1$ (in eenheden $OE$)?
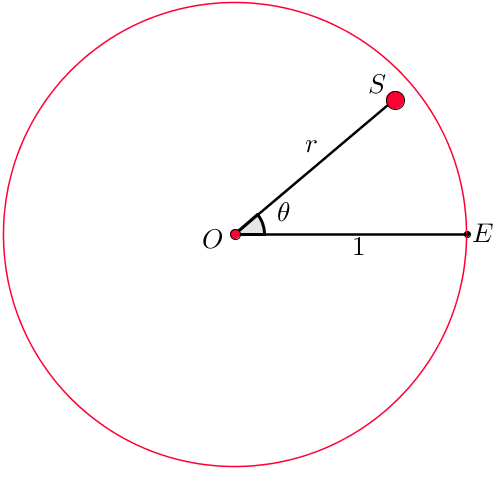
Zoals voorheen verdubbelt de hoek $\theta$ dagelijks. We spreken nu extra af dat de afstand $r$ (in eenheden $OE$) elke dag kwadrateert. Kortom, de baan van $S$ krijgen we door te itereren met:
$$
f(r;\; \theta)=(r^2;\; 2\theta).
$$
Om te benadrukken dat we hier niet met gewone coördinaten werken maar met een afstand en een hoek hebben we $r$ en $\theta$
gescheiden door een punt-komma. De getallen $r$ en $\theta$ worden de poolcoördinaten van het het punt $S$ genoemd.
De formule $f(r;\; \theta)=(r^2;\; 2\theta)$ geldt overigens ook voor satellieten die niet uit koers zijn. Voor een punt $z$ op de cirkel met middelpunt $O$ en straal $OE$ geldt namelijk:
$$
z=(1; \; \theta),
$$
en dus
$$
f(z)= (1^2; \; 2\theta)=(1; \; 2\theta).
$$
Punten op de cirkel gedragen zich bij iteratie met $f(r;\; \theta)=(r^2;\; 2\theta)$ dus precies zoals we willen.
Hoe de formule $f(r;\; \theta)=(r^2;\; 2\theta)$ uitpakt voor de startwaarde $z_0=(\frac{9}{10};\; 40^{\circ})$ zie je hieronder:
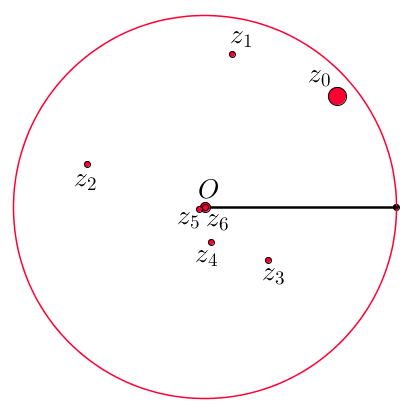
De bijbehorende berekening voor $z_1$ tot en met $z_6$ is:
$$
z_1=((\frac{9}{10})^2;\; 2\cdot 40^{\circ})=(\frac{81}{100};\; 80^{\circ}).
$$
$$
z_2=((\frac{81}{100})^2;\; 2\cdot 80^{\circ})=(\frac{6.561}{10.000};\; 160^{\circ}).
$$
$$
z_3=((\frac{9}{10})^{8};\; -40^{\circ})=(\frac{43.046.721}{100.000.000}; \; -40^{\circ}).
$$
en zo verder tot:
$$ z_6 = ({\tiny\frac{11.790.184.577.738.583.171.520.872.861.412.518.665.678.211.592.275.841.109.096.961}{10.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000}}; \; 40^{\circ}).
$$
Je ziet dat door het kwadrateren het aantal decimalen snel toeneemt.
Veel software, zoals ook GeoGebra, werkt met 15 decimalen.
Dit betekent dat je altijd op je hoede moet zijn of de door een computer gemaakte afrondfout nog tolerabel is.
We zullen later meemaken dat het faliekant misgaat!
Het lijkt er overigens op dat na 6 dagen de satelliet neerstort op Origo: de positie van $z_6$ ligt over de planeet.
Als we echter $O$ en $z_6$ als wiskundige punten beschouwen is de sateliet er nog steeds ongeveer $0,001$ vandaan.
Zo bezien bereikt de satelliet de planeet nooit helemaal.
Als we de bovenstaande berekening namelijk voorzetten vinden we de directe formule
$$
z_n= ((\frac{9}{10})^{2^n};\; 2^n\cdot 40^{\circ}).
$$
Hieraan zien we dat baan van $z_0$ convergeert naar $O$, ofwel:
$$
\lim_{n\rightarrow\infty}z_n=O.
$$
Een aantrekkend en een afstotend vast punt
Eerder zagen we dat een convergente baan alleen een vast punt als limiet kan hebben.
Wat zijn de vaste punten van $f(r;\; \theta)=(r^2;\; 2\theta)$ ?
Dan moet in ieder geval gelden:
$$
r^2=r,
$$
ofwel
$$
r=0 \; \text{of} \; r=1.
$$
Vanwege de hoekverdubbeling blijven als vaste punten over:
$$
O \text{ en } (1;\; 0^{\circ}).
$$
Van deze twee is $O$ aantrekkend en $(1;\; 0^{\circ})$ afstotend. Wat bedoelen we hiermee? Eerst iets over de notatie.
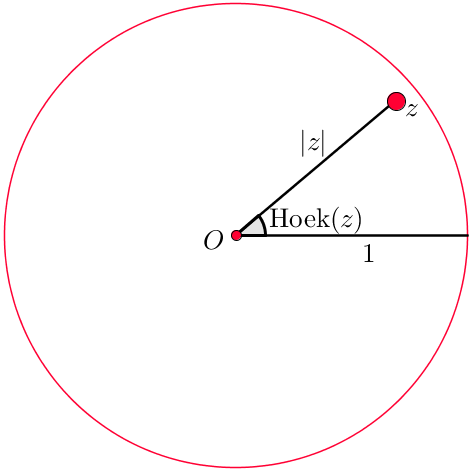
Soms schrijven we in plaats van $r$ en $\theta$ liever $|z|$ en Hoek($z$).
Misschien is het vreemd om hier een absolute waarde te zien, maar net als dat
$$
|-3|=3,
$$
wil zeggen dat de afstand op de getallenlijn van $-3$ tot $0$ gelijk is aan $3$, bedoelen we met $|z|$ de afstand van $z$ tot $O$.
We kunnen $f(r;\; \theta)=(r^2;\; 2\theta)$ dus ook schrijven als:
$$
f(z)=(|z|^2;\; 2\cdot \mathrm{Hoek}(z)).
$$
Nu komen we terug op de bewering dat $O$ een aantrekkend vast punt is.
Stel namelijk dat $|z_0|<1$.
Dan geldt
$$
\lim_{n\rightarrow\infty}|z_0|^{2^n}=0,
$$
en dus
$$
\lim_{n\rightarrow\infty}f^n(z_0)=O.
$$
Elk punt binnen de eenheidscirkel convergeert dus naar $O$. Het punt $O$ fungeert als een soort doucheputje waar elke punt binnen de eenheidscirkel naartoe stroomt.
Voor punten in de buurt van $(1;\ \ \ 0^{\circ})$ zijn er drie mogelijkheden: de baan convergeert naar $O$, de baan beweegt op de cirkel of de baan verdwijdert zich steeds verder van $O$. Het karakter van dit vaste punt is dus anders dan dat van $O$. Vanaf Week 3 lees je meer over aantrekkende en afstotende vaste punten en kom je erachter wat deze te maken hebben met de Mandelbrotverzameling.
De verboden cirkel $V$
Als een satelliet buiten de cirkel met straal 1 start zal hij snel ver van de planeet raken.
Reddingswerkers worden dan ingezet om de satelliet op te pikken.
Als de satelliet echter buiten de cirkel $V$ met straal 2 en middelpunt $O$ komt wordt de satelliet als verloren beschouwd.
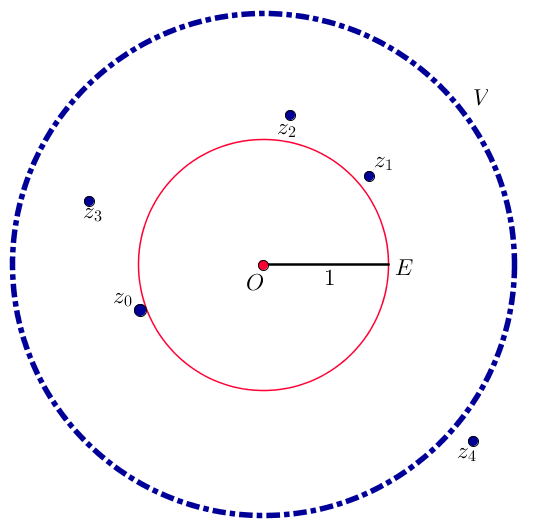
In het plaatje hierboven zien we dat het voor $z_0=(1,05;\; 200^{\circ})$ al mis gaat na 4 dagen. Er geldt namelijk:
$$
z_4=((1,05)^{16};\; 16\cdot 200^{\circ})\approx (2,2; \; -40^{\circ}).
$$
Samenvatting
Deze pagina bestudeerde iteratie van de functie
$$
f(|z|;\; \text{Hoek(}z\text{)} )=(|z|^2;\; 2\cdot \text{Hoek(}z\text{)}).
$$
Hierbij is $|z|$ de absolute waarde
van $z$, oftewel de afstand van $z$ tot $O$.
Verder is $\; \text{Hoek(}z\text{)}=\angle zOE$.
Binnen de cirkel met straal 1 convergeert de baan naar het aantrekkende vaste punt $O$.
Daarbuiten ontsnapt de baan naar het oneindige. De cirkel met straal 1 kun je dus zien als de grens tussen begrensde en onbegrensde banen.
In de onderstaande dynamische afbeelding zie je dit door te slepen met de startwaarde $z_0$.